Convex Analysis and Optimization
Dr. Peter Ochs|
Many problems in image processing, computer vision, and machine learning can be formulated as convex optimization problems and can be solved efficiently. The development of fast optimization algorithms relies on the knowledge of convex analysis. In this lecture, the basics of convex analysis are introduced, where we will attach importance to the geometric interpretation. Moreover, the connection between theory and applications will be explored in programming exercises from image processing and machine learning.
This mathematical lecture introduces the basic terminology and tools from convex analysis, such as convex functions/sets, relation between sets and functions, the Projection Theorem, Moreau envelope and proximal mapping, the subdifferential and optimality conditions of (nonsmooth) convex functions, and some basic duality theory. This first part of the lecture is complemented with some simple algorithms. The focus of the second part is efficient convex optimization algorithms and their complexity estimates.
|
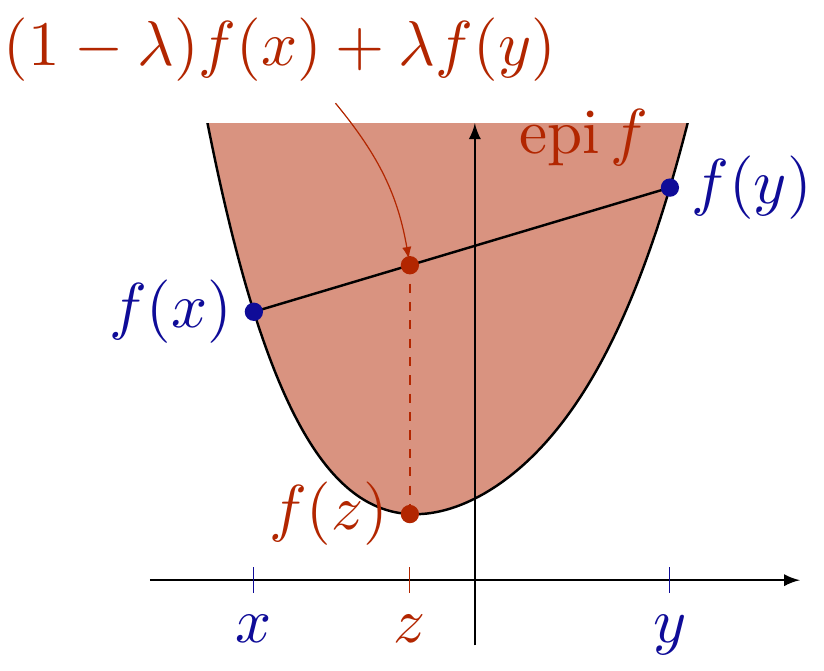
|
News:
| 26.10.2016: | First version of the lecture notes is online. (See below.) |
| 31.10.2016: | Tutorials on Wednesdays are cancelled. For feedback on the exercises, please come to the office of Peter Ochs or Mohammadreza Zolfaghari. Extra tutorial sessions will be announced here. Please check this web page from time to time. |
| 31.10.2016: | Peter Ochs is away from 14.11. to 18.11. The lecture on 14.11.2016 is postponed to the tutorial on 23.11.2016. |
| 09.01.2017: | There is no lecture on 06.02.2017. |
| 30.01.2017: | The date for the oral exam is: 23.03.2017. |
| 07.03.2017: | Schedule for the oral exam on 23.03.2017 in room 01-020, building 052: 10:30-11:00: Baumgärtner Katrin 11:00-11:30: Striet Ludwig 11:30-12:00: Bhatt Aditya Note: By default, the exam will be in English. In case you prefer German, please contact Peter Ochs. |
Slides:
Class 0 (17.10.): Introduction and basic concepts of complexityClass 1 (24.10.): Lipschitz continuity and the Gradient Descent Method
Class 2 (31.10.): Terminology of Variational Analysis
Class 3 (7.11.): Convex sets and the Projection Theorem
Class 4 (21.11.): Convex functions
Class 5 (23.11.): Moreau envelope and Proximal Mapping
Class 6 (28.11.): Moreau envelope and Proximal Mapping II
Class 7 (5.12.): The subdifferential and Fermat's rule
Class 8 (12.12.): Lower complexity bounds
Class 9 (19.12.): The Gradient Method for smooth convex optimization
Class 10 (9.1.): Nonsmooth convex optimization
Class 11 (16.1.): Geometric introduction to duality
Class 12 (23.1.): Applications of convex duality
Class 13 (30.1.): Summary
Class 14 (6.2.): cancelled
Download Lecture Notes (Version 23.01.2017).
Exercise material:
Theoretical and practical exercises (in Matlab).Exercise material will appear here.
Exercise 0 (19.10.)
Exercise 1 (26.10.)
Exercise 2 (02.11.)
Exercise 3 (09.11.)
Exercise 4 (21.11.)
Exercise 5 (23.11.)
Exercise 6 (30.11.)
Exercise 7 (07.12.)
Exercise 8 (14.12.): same as Exercise 7
Exercise 9 (21.12.): catch up with all previous exercises
Exercise 10 (11.01.)
Exercise 11 (18.01.)
Exercise 12 (25.01.): catch up with all previous exercises
Exercise 13 (01.02.): catch up with all previous exercises
Exercise 14 (08.02.) cancelled


