|
|
|
|
|
|
|
This article has also been translated to Serbo-Croatian language by Jovana Milutinovich from Geeks Education. What is frog on hand?frog on hand is name of our on-line handwriting recognition project. The name is an acronym for "freiburg recognition of on-line handwriting". Several researches at the University of Freiburg have contributed developing it (please refer to the section of honor). This web page aims to give a concise description of the recognition. It gives some explanations, visualizations and links into literature. A rough division of the recognition system frog on hand can be made into four main modules. Those are dealing with In the following description, each of those modules will be briefly addressed. If you are interested in a real-life application, don't miss the description of frog on hand's character recognition on a Compaq iPAQ. Most of the images on this web page are displayed in a down-sampled resolution. You can get a larger view of the images by clicking on them. We have included some multi-media animations. You have the choice to play these in one of the following formats and codecs:
|
||||||||||||||
"What is on-line handwriting recognition?" and "Where to get data?"A precise definition of handwriting recognition (HWR) is given in [Plamondon and Srihari, 2000]:
On-line HWR, in contrast to off-line HWR, refers to the situation where the recognition is performed concurrent to the writing process. This distinction has some consequences, regarding further differentiations between on-line and off-line HWR. Among others, these pertain important aspects like data acquisition, data representation, recognition methods and typical applications. So, what is specific about on-line handwriting data? Again, here is a rather complicated, but precise definition:
Often, simply a sequence p=[(x1,y1),...,(xN,yN)] of x-y-coordinates (xi,yi) is used to describe on-line handwriting data (see figures 1 and 3). Very typical applications for on-line HWR concern user interfaces of personal digital assistants (PDAs), smart phones or Microsoft's new tablet PCs. Contrary to on-line HWR, off-line HWR is usually performed some time after creation. In this context data is usually represented as a pixel matrix, e.g. as a scanned image (see figure 2). A typical off-line application is the automatic recognition of postal address fields or bank checks. Our specific research is dealing with on-line handwriting recognition. The largest and most popular non-proprietary database of on-line handwriting is the UNIPEN database. Its current release comprises about 60,000 lower case characters, 30,000 upper case characters, 15,000 numerals, 85,000 words and 15,000 free text segments. |
|||||||||||||||
Pre-processingThe HWR system frog on hand includes a pre-processing of the handwriting data. It comprises 3 steps:
More detailed information about the pre-processing is given in [Simon, 2002]. |
|||||||||||||||
Feature selectionfrog on hand employs a local feature representation. Depending on the application, the following features are computed either from the re-sampled or from the original writing:
Thus, posterior to feature selection we have a sequence of three-dimensional feature vectors. Figure 5 shows an example feature sequence. A more detailed depiction of the feature extraction is included in the publications [Bahlmann and Burkhardt, 2004] and [Simon, 2002]. |
|||||||||||||||
ClassificationPre-processing and feature selection have transformed the handwriting data (i.e. a sequence of x-y-coordinates) into a sequence of three-dimensional feature vectors (as illustrated in figure 5). For a recognition, the feature sequence is to be presented to a pattern classifier. We have developed two complementary classifier approaches, each one having its individual strong points. In order to cope with temporal variations, both make use of the dynamic time warping (DTW) (also known as elastic matching) concept. However they pursue quite different classification philosophies. The first approach employs a generative principle and is called cluster generative statistical DTW (CSDTW). The second approach is using a discriminative method, as it is based on the support vector machine (SVM). We have developed a specifically adjusted SVM-kernel: the Gaussian DTW kernel. The classification method is thus called SVM-GDTW. |
|||||||||||||||
|
Classification with CSDTWCSDTW (cluster generative statistical dynamic time warping) is our extension of the dynamic time warping (DTW) classification. CSDTW supplements DTW by a holistic combination of a cluster analysis and a probabilistic / statistical modeling. What is DTW?DTW is a concept that allows an elastic match of two sequences. Figure 6 gives a graphical illustration of an example elastic match: Given two vector sequences (in the following called "test" and "reference" sequence), DTW aims to identify (or align) corresponding sample points among test and reference sequence, as is shown with the two instances of the "3". In this respect, the matching is not a linear point-by-point matching, but it is elastic. In DTW classification, the recognition of a character is performed with help of the so-called Viterbi algorithm. It can be summarized by the following two main aspects:
The classification itself is then performed pursuing a minimum distance philosophy by computing the Viterbi distance of the test sequence to every element in a set of reference sequence templates. What is CSDTW, frog on hand's extension of DTW?CSDTW uses a generalization of the DTW distance as the underlying distance measure. Additionally, it aims to treat writing variations by a holistic combining of cluster analysis and statistical sequence modeling. To be more precise, the cluster analysis is employed with the aim of identifying different character "shapes" or "styles" (which are called allographs in HWR research) in the training set of characters (see figure 11 to see different styles of a character "b"). Based on the clusters identified, statistical sequence reference models are estimated. Each of those corresponds to a sequence of probability density functions (PDFs), one PDF for every re-sampled point. Simple multivariate Gaussians are used (see figure 8) as PDF basis functions. In this respect, CSDTW shares common ideas with hidden Markov modeling (HMM). Contrary to previous attempts of combining clustering and statistical sequence modeling, CSDTW uses a single feature space and a closely related dissimilarity measure for the cluster analysis and the statistical modeling. A special treatment for the statistical modeling is necessary, as one of the features, the tangent slope angle, is a directional variable. We cope with this problem by modeling the feature space with a specifically adapted PDF, the multivariate semi-wrapped Gaussian distribution (see [Bahlmann, 2004]). Figure 7 and movie 1 illustrate an example CSDTW classification. More detailed information about the CSDTW framework is given in the publications [Bahlmann and Burkhardt, 2004], [Bahlmann, 2004] and [Bahlmann and Burkhardt, 2001]. |
||||||||||||||
|
Classification with SVM-GDTWOur current "hot" topic is the incorporation of discriminative power into HWR. We address this issue by the utilization of support vector machine (SVM) classifiers. In this respect, the aim is to develop an SVM kernel that is adjusted for the use with sequential data: the result so far is the Gaussian dynamic time warping (GDTW) kernel. What is an SVM?An SVM classifier discriminates two classes of feature vectors by generating hyper-surfaces in the feature space, which are "optimal" in a specific sense: The hyper-surface obtained by the SVM optimization is guaranteed to have the maximum distance to the "nearest" training examples, the support vectors. This principle is sketched in figure 9 for a two-dimensional, linearly separable example. Chih-Jen Lin provides an instructive, interactive Java demo for two-dimensional data on his WWW page. An important property of SVMs is that they do not directly operate on the feature vectors Pi or Pj, but instead on kernel evaluations K(Pi,Pj) of them. E.g., the classification of a test pattern T is performed by evaluating a weighted sum of kernel evaluations of T with each support vector Si, y = sumi( ai * K(T,Si) ) and assigning the "positive" or "negative" class for T depending on the sign of y. What is special about frog on hand's SVM-GDTW?However, usual SVM kernels are designed to deal with data that is embedded in a vector space of fixed dimension. Since on-line handwriting data is not of a fixed dimension, but of a variable-length sequential form, SVMs cannot be applied to HWR with the usual methods. We have addressed this issue by developing an appropriate SVM kernel that is defined for sequential data: the Gaussian dynamic time warping (GDTW) kernel (thus the acronym SVM-GDTW). In figure 10 and movie 2 a few typical support vectors and kernel evaluations with our GDTW kernel are illustrated. How does frog on hand's SVM-GDTW deal with the multi-class issue?A basic SVM discriminates between only two classes. However, some general approaches for combining two-class SVMs into a multi-class SVM have been developed. We use the DAG (decision directed acyclic graph)-SVM approach for this issue. More detailed information about our SVM classifier and references for general SVM issues are given in the award-winning publication [Bahlmann et al., 2002]. |
||||||||||||||
TrainingBoth classification methods (CSDTW and SVM-GDTW) come with powerful training algorithms. Generally, the purpose of the training is
A large dataset extremely improves the accuracy of the obtained classifiers. frog on hand's underlying dataset for this issue is the UNIPEN on-line handwriting database. |
|||||||||||||||
CSDTW trainingCSDTW training comprises the cluster analysis and the estimation of statistical sequence parameters. Generating allograph prototypes by hierarchical clusteringFor each character class an agglomerative hierarchical clustering algorithm identifies a set of clusters. Figure 11 shows an example of the so-called dendrogram of the hierarchical clustering. As a result of the clustering, each cluster is given by
The clustering algorithm uses a dissimilarity measure that is closely related to the one used for classification and parameter estimation. Thus, clusters found in the cluster space correspond to well-formed clusters in the classifier space. Estimating the statistical model parameters by Viterbi trainingFor each cluster the parameters of the PDF sequences are trained by the iterative Viterbi training. The initialization problem can be solved in a data-driven fashion. The parameters of the PDFs, which are represented by multivariate Gaussians, are initialized as follows:
This configuration is the initial "model". The iterative training is an alternation of the following two steps:
Detailed descriptions of the CSDTW training and the reference models are given in the publications [Bahlmann and Burkhardt, 2004] and [Bahlmann and Burkhardt, 2001]. |
|||||||||||||||
SVM-GDTW trainingThe SVM training is performed by the standard sequential minimal optimization (SMO). We don't have to care about the special form of the sequential data, since the training does not directly operate on the feature vectors Pi or Pj, but solely on kernel evaluations K(Pi,Pj). More detailed information about our SVM-GDTW training is given in the award-winning publication [Bahlmann et al., 2002] |
|||||||||||||||
Experiments on the UNIPEN databaseWith the methods described above we achieve the following character recognition error rates on UNIPEN data:
These include the lowest rates reported on UNIPEN data. For a more thorough description of the experiment's environment and a comparison with other state-of-the-art handwriting recognizers see [Bahlmann et al., 2002] and [Bahlmann and Burkhardt, 2004]. |
|||||||||||||||
|
ApplicationsWe have implemented the frog on hand character recognition using the CSDTW classification on a PDA, a Compaq iPAQ 3660 (see Figure 12). It is operated by a Linux kernel 2.4.18 from the Familiar distribution, the graphical user interface is the Open Palmtop Integrated Environment (OPIE), which is a GPL licensed fork of Trolltech's Qtopia. Using the approach described in the sections above, the implementation is an integrated character recognition plug-in that runs both inside Qtopia and OPIE. The character label recognized by the plug-in is handed over to the active application (e.g. date book, address book, to-do list, etc.). Movie 4 gives an impression. Contrary to the implementation in our development environment, a fixed point data representation is used on the PDA, since the StrongARM processor lacks a built-in floating point arithmetic. The classification of a character approximately takes 0.3 seconds in average on the iPAQ. However, due to the rich representation of the reference models, the models occupy a rather large amount of flash space. Together with the program ~2.5 MByte are required :( Feel free to test the plug-in on your PDA. A binary (packaged as an ipk; both Linux Compaq iPAQ and Sharp Zaurus are supported) is available from our feed. |
||||||||||||||
Links and ToolsValuable starting links for the techniques used for frog on hand are
Some tools and links, with help of which frog on hand was developed:
|
|||||||||||||||
HonorThe team which has developed frog on hand :
|
last modified
|
|

![frog on hand - On-line data [move to restart animation]](images/mov/char-t-anim-gross.gif)
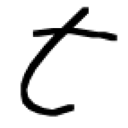
![Sample "b" [click for a larger view]](images/figures/b-sample-128x128.gif)
![Spline approximation and re-sampling [click for a larger view]](images/figures/b-resampling-128x128.gif)
![Feature selection [click for a larger view]](images/figures/b-feature-vx-vy-theta_spline-128x128.gif)
![frog on hand - Dynamic time warping [click for larger view]](images/figures/matching-combined10-lr.gif)
![frog on hand - Viterbi alignment [click for a larger view]](images/figures/viterbi-alignment-128x128.gif)
![Reference pattern "h" [click for a larger view]](images/figures/h-reference-vx-vy-128x128.gif)
![SDTW classification [click for a larger view]](images/figures/hwr_demo_dtw_lr.gif)
![two dimensional SVM [click for larger view]](images/figures/svm-2d-libsvmtl-128x128.gif)
![DAG-SVM [click for larger view]](images/figures/svmseq-lr.gif)
![clustering [click for larger view]](images/figures/b-clustering-wrapper-128x128.gif)
![Compaq demo [click for larger view]](images/photos/frog-on-ipaq-lr.jpg)
![frog on ipaq [click for a larger view]](images/mov/frog-on-ipaq-still-lr.gif)